Abaqus tutorials Abaqus tutorials
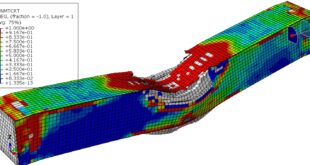
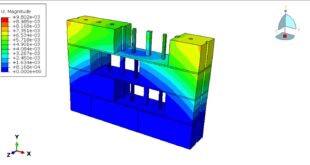
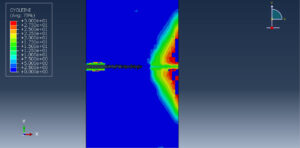
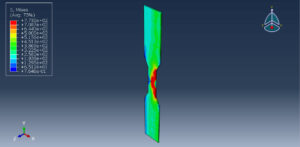
In this tutorial, the Simulation of low cyclic fatigue damage based on hysteresis energy on Abaqus has been investigated. The steel plated is modeled as a two-dimensional part. You can see a figure of the assembled part below.
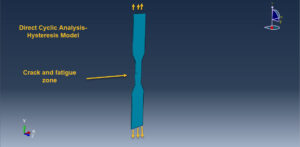
It is well known that after a number of repetitive loading cycles, the response of an elastic-plastic structure, such as an automobile exhaust manifold subjected to large temperature fluctuations and clamping loads, may lead to a stabilized state in which the stress-strain relationship in each successive cycle is the same as in the previous one. The classical approach to obtain the response of such a structure is to apply the periodic loading repetitively to the structure until a stabilized state is obtained. This approach can be quite expensive, since it may require the application of many loading cycles before the stabilized response is obtained. To avoid the considerable numerical expense associated with a transient analysis, a direct cyclic analysis can be used to calculate the cyclic response of the structure directly.
In the direct cyclic analysis, the Fourier representation of the solution and the residual vector to obtain the stabilized cyclic response directly. The damage initiation criterion is a phenomenological model for predicting the onset of damage due to stress reversals and the accumulation of inelastic strain in low-cycle fatigue analysis. Once the damage initiation criterion is satisfied at a material point, the damage state is calculated and updated based on the accumulated inelastic hysteresis energy density per cycle, for a stabilized cycle. The rate of the damage in a material point per cycle is given by
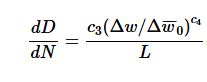
Abaqus uses the above damage initiation and evolution based on Hysteresis energy in the direct cyclic loading. Damage evolution for ductile materials can be defined for any element that can be used with the damage initiation criteria for a low-cycle fatigue analysis in Abaqus/Standard
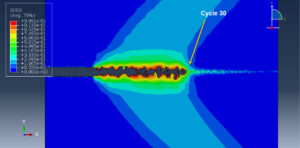
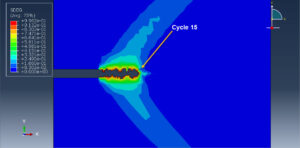
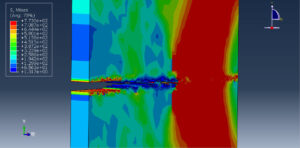
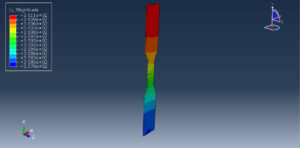
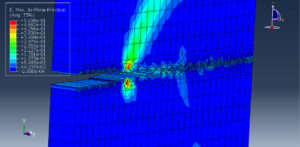
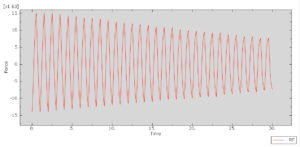
You can see below the results for the steel plate under thirty cycles by using the Hysteresis energy method as the code files.
