Simulation fatigue phenomenon of the steel plate in Abaqus by using direct cyclic step

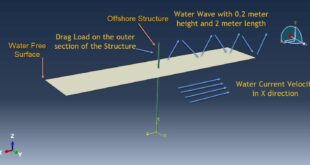
In this tutorial Simulation fatigue phenomenon of the steel plate in Abaqus by using direct cyclic step has been investigated.Two dimensional part for steel and wire part to define initial crack length has been used . Elastic material couple with traction separation law to consider the fracture and crack growth in the plate has been implied. You can see a figure of the assemble parts at below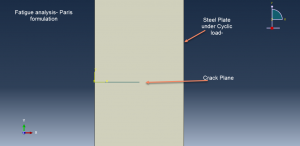

It is well known that after a number of repetitive loading cycles, the response of an elastic-plastic structure, such as an automobile exhaust manifold subjected to large temperature fluctuations and clamping loads, may lead to a stabilized state in which the stress-strain relationship in each successive cycle is the same as in the previous one. The classical approach to obtain the response of such a structure is to apply the periodic loading repetitively to the structure until a stabilized state is obtained. This approach can be quite expensive, since it may require the application of many loading cycles before the stabilized response is obtained. To avoid the considerable numerical expense associated with a transient analysis, a direct cyclic analysis can be used to calculate the cyclic response of the structure directly. The basis of this method is to construct a displacement function  that describes the response of the structure at all times t during a load cycle with period T.A truncated Fourier series is used for this purpose

where n stands for the number of terms in the Fourier series,  is the angular frequency, and , and  are unknown displacement coefficients associated with each degree of freedom in the problem. Abaqus/Standard solves for the unknown displacement coefficients by using a modified Newton method, with the elastic stiffness matrix at the beginning of the analysis step serving as the Jacobian in the scheme. We expand the residual vector in the modified Newton method using a Fourier series of the same form as the displacement solution

The number of Fourier terms required to obtain an accurate solution depends on the variation of the load as well as the variation of the structural response over the period. In determining the number of terms, keep in mind that the objective of this kind of analysis is to make low-cycle fatigue predictions. Hence, the goal is to obtain good approximation of the plastic strain cycle at each point; local inaccuracies in the stresses are less important. More Fourier terms usually provide a more accurate solution but at the expense of additional data storage and computational time. In addition, an accurate integration of the Fourier residual coefficients requires that the residual vector be evaluated at an adequate number of time points during the cycle. Abaqus/Standard uses a trapezoidal rule, which assumes a linear variation of the residual over a time increment, to integrate the residual coefficients. For accurate integration the number of time points must be larger than the number of Fourier coefficients (which is equal to , where n represents the number of Fourier terms). Abaqus/Standard will automatically reduce the number of Fourier coefficients used for the next iteration if it is found to be greater than the number of increments taken to complete an iteration

In this simulation 150 cycle has been used. To define crack growth XFEM procedure has been implied. To use surface fatigue behavior Paris low couple with power low criterion has selected.The onset and crack growth are characterized by using the Paris law, which relates the relative fracture energy release rates to crack growth rates. The Paris regime is bounded by the energy release rate threshold, , below which there is no consideration of fatigue crack initiation or growth, and the energy release rate upper limit, , above which the fatigue crack will grow at an accelerated rate.  is the critical equivalent strain energy release rate calculated based on the user-specified mode-mix criterion and the fracture strength of the bulk material. The formulae for calculating  have been provided above for different mixed mode fracture criteria. You can specify the ratio of  over  and the ratio of  over .The Paris low definition has shown in the below figure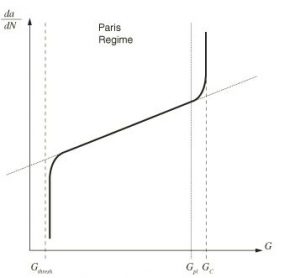

The power law model is described in Wu and Reuter (1965) by the following formula

The onset of fatigue crack growth refers to the beginning of fatigue crack growth at the crack tip in the enriched elements. In a low-cycle fatigue analysis the onset of the fatigue crack growth criterion is characterized by , which is the relative fracture energy release rate when the structure is loaded between its maximum and minimum values. The fatigue crack growth initiation criterion is defined as

where  and  are material constants and  is the cycle number. The enriched elements ahead of the crack tips will not be fractured unless the above equation is satisfied and the maximum fracture energy release rate, , which corresponds to the cyclic energy release rate when the structure is loaded up to its maximum value, is greater than 

Once the onset of the fatigue crack growth criterion is satisfied at the enriched element, the crack growth rate, , can be calculated based on the relative fracture energy release rate, . The rate of the crack growth per cycle is given by the Paris law if 

where  and  are material constants.If , the enriched elements ahead of the crack tips will be fractured by increasing the cycle number count, , by one only

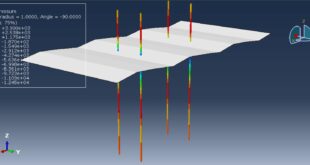
You can see some figures of this simulation at below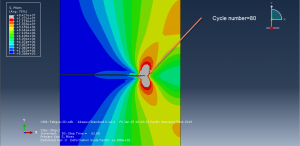

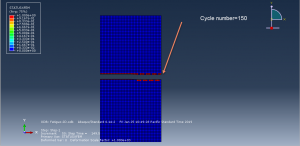
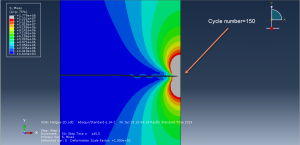
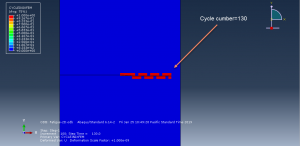
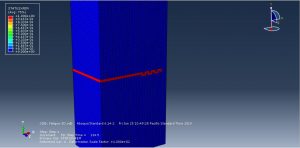
You can provide CAE ,INP,and English video files of this simulation here. The cost of these files is Twenty-Six Euros. you can click on the bellow bottom to beginning process

You can purchase the tutorial through a PayPal account, a Visa, or a Master card,  just before payment,send me an email to this address: karampourp@gmail.com